2016.7.18 名古屋市営地下鉄最小距離完乗
これは何ですか
ある路線網において、「その路線網を通り、必ず全区間を1回以上通って出発駅まで戻ってくる」ことを考える。この移動距離が最小となる通り方を求める問題は中国人郵便配達問題と呼ばれる。これを名古屋市営地下鉄で実践したものである。
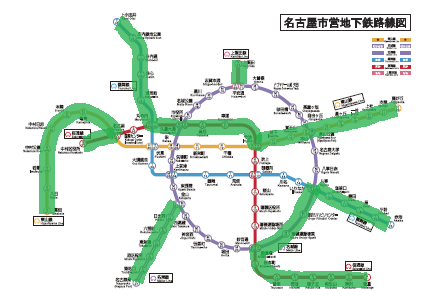 ←名古屋市営地下鉄の最小距離完乗の方法。太線の区間は2回、細線の区間は1回乗ればよい。
←名古屋市営地下鉄の最小距離完乗の方法。太線の区間は2回、細線の区間は1回乗ればよい。
旅行記
名古屋市営地下鉄最小距離完乗 - SlideShare(2016.7.23の勉強会「わんくま同盟 名古屋勉強会 #39」におけるライトニングトーク資料)
計算方法
- Maraigueのメモ倉庫 - 名古屋市営地下鉄を最小距離の乗車で「乗りつくして出発駅に戻る」(旅行実施前に最小距離での乗車方法を計算したもの)
- Boost.GraphでJR全線乗り尽くしプランを立てる - SlideShare(詳細 & C++での実装。ソースコードあり。2014.7.12の勉強会「プログラミング生放送+CLR/H+Sapporo.cpp 勉強会@札幌」における発表資料)
要約すると以下の通りです。
- どの駅間を2回乗り、どの駅間を1回乗るかだけ決めればよい(3回以上乗る必要のある区間は存在しない)。
- 橋(もしなくなると路線網が分断されるような区間。行き止まりになるような区間など)は2回乗ると確定させる。
- 橋をすべて除外した路線網を見たときに、路線が奇数方向に伸びる駅だけを集めてくる。名古屋市営地下鉄の場合は「丸の内」「本山」「八事」「新瑞橋」の4駅。
- これらの駅を2駅ずつの組にしたとき、「組の間での移動距離」の合計が最小になる組み合わせを見つける。その組の経路は2回通るが、それ以外は1回通ればよい。今回の場合は「丸の内-本山」+「八事-新瑞橋」と組み合わせるのが最小となる。
- 「組の間での移動距離」を計算するときや、その区間を2回通ると決定するときは、それが最小距離となるような経路で選ばないとならないことに注意が必要。例えば上記で示したうちの「丸の内-本山」は、「丸の内-(桜通線)-今池-(東山線)-本山」と通るのが最小距離なので、2回通る区間もそう選ばないとならない。